HiHoCoder: 九宫
From:[Offer收割]编程练习赛1
描述
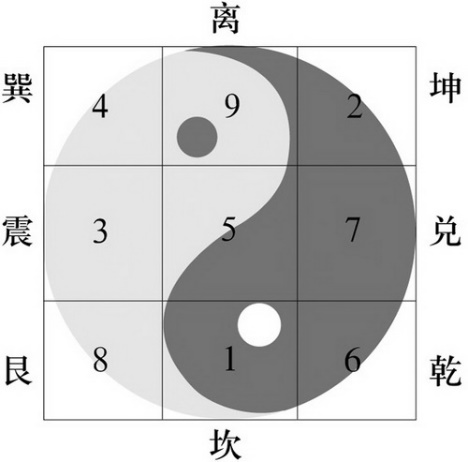
小Hi最近在教邻居家的小朋友小学奥数,而最近正好讲述到了三阶幻方这个部分,三阶幻方指的是将1~9不重复的填入一个3*3的矩阵当中,使得每一行、每一列和每一条对角线的和都是相同的。三阶幻方又被称作九宫格,在小学奥数里有一句非常有名的口诀:“二四为肩,六八为足,左三右七,戴九履一,五居其中”,通过这样的一句口诀就能够非常完美的构造出一个九宫格来。
有意思的是,所有的三阶幻方,都可以通过这样一个九宫格进行若干镜像和旋转操作之后得到。现在小Hi准备将一个三阶幻方(不一定是上图中的那个)中的一些数组抹掉,交给邻居家的小朋友来进行还原,并且希望她能够判断出究竟是不是只有一组解。
而你呢,也被小Hi交付了同样的任务,但是不同的是,你需要写一个程序~
输入
输入仅包含单组测试数据。每组测试数据为一个3*3的矩阵,其中为0的部分表示被小Hi抹去的部分。
对于100%的数据,满足给出的矩阵至少能还原出一组可行的三阶幻方。
输出
如果仅能还原出一组可行的三阶幻方,则将其输出,否则输出“Too Many”(不包含引号)。样例输入
2
3
0 5 0
0 3 0样例输出
2
3
1 5 9
8 3 4
使用回溯法进行求解。
还是做题少了,不够敏锐。知道用回溯的话写代码还好,一旦想偏就怎么也拉不回来了……
AC代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iostream>
using namespace std;
int Nine[9];
int a, b, c;
int* addr = Nine;
int nums = 0;
int o2nine[10] = { 0,1,2,3,4,5,6,7,8,9 };
int present[9];
#define index(r,c) ((r) * (3)+(c))
bool check()
{
int r = 0;
r = Nine[index(0, 0)] + Nine[index(0, 1)] + Nine[index(0, 2)];
if (r > 15) return false; r = 0;
r = Nine[index(1, 0)] + Nine[index(1, 1)] + Nine[index(1, 2)];
if (r > 15) return false; r = 0;
r = Nine[index(2, 0)] + Nine[index(2, 1)] + Nine[index(2, 2)];
if (r > 15) return false; r = 0;
r = Nine[index(0, 0)] + Nine[index(1, 0)] + Nine[index(2, 0)];
if (r > 15) return false; r = 0;
r = Nine[index(0, 1)] + Nine[index(1, 1)] + Nine[index(2, 1)];
if (r > 15) return false; r = 0;
r = Nine[index(0, 2)] + Nine[index(1, 2)] + Nine[index(2, 2)];
if (r > 15) return false; r = 0;
r = Nine[index(0, 0)] + Nine[index(1, 1)] + Nine[index(2, 2)];
if (r > 15) return false; r = 0;
r = Nine[index(0, 2)] + Nine[index(1, 1)] + Nine[index(2, 0)];
if (r > 15) return false;
return true;
}
void cal(int x)
{
bool allZero = true;
for (int i = 1; i < 10; ++i)
{
if (o2nine[i] != 0)
{
allZero = false;
}
}
if (allZero)
{
++nums;
for (int i = 0; i < 9; ++i)
{
present[i] = Nine[i];
}
return;
}
if (Nine[x] == 0)
{
for (int i = 1; i < 10; ++i)
{
if (o2nine[i] != 0)
{
Nine[x] = i;
o2nine[i] = 0;
if (check())
{
cal(x+1);
}
Nine[x] = 0;
o2nine[i] = i;
}
}
}
else
{
cal(x+1);
}
}
int main(int argc, char** argv)
{
for (int i = 0; i < 3; ++i)
{
cin >> a >> b >> c;
addr[0] = a;
addr[1] = b;
addr[2] = c;
addr += 3;
o2nine[a] = 0;
o2nine[b] = 0;
o2nine[c] = 0;
}
Nine[index(1, 1)] = 5;
o2nine[5] = 0;
cal(0);
if (nums == 1)
{
for (int i = 0; i < 3; ++i)
{
for (int j = 0; j < 3; ++j)
{
cout << present[index(i, j)] << " ";
}
cout << endl;
}
}
else
{
cout << "Too Many" << endl;
}
return 0;
}